Reputation evaluation for P2P communities via temporal PageRank
During my PhD I co-created with Prof. Wolfgang-Karl Härdle, Raul Bag, and Julian Winkel, Quantinar, a peer-to-peer platform which enhances research collaboration and reproducibility across various scientific fields including Fintech, Blockchain, and Data Science. We wrote an article, Quantinar: A Blockchain p2p Ecosystem for Scientific Research, presenting the scientific innovation of the platform available on SSRN and currently under review in the Journal of Computational Statistics.
Quantinar positions itself as a revolutionary platform by offering a decentralized architecture where knowledge, data, and code are interconnected, providing a comprehensive scientific research and education environment. It promotes open science by ensuring that publications are reproducible through the integration of articles with their corresponding datasets and code, thus addressing issues like publication bias and the lack of transparency in traditional academic publishing.
Quantinar aims to redefine how scientific knowledge is created, shared, and validated, leveraging blockchain technology to ensure integrity and openness in research. It represents a shift towards a more collaborative and transparent academic ecosystem, where the barriers between data producers and consumers are diminished, fostering a cycle where today’s learners can become tomorrow’s innovators.
Quantinar also introduces a novel peer-review process that utilizes a game theory-based approach to incentivize impartial and efficient reviews, aiming to make the review process more equitable and less susceptible to biases that plague traditional peer review systems. The platform supports a community-driven approach where contributors are rewarded through a sophisticated algorithm inspired by PageRank, recognizing the value of contributions in a dynamic and scalable manner.
I was specifically in charge of developing the reputation evaluation system.
Problem
Traditional reputation systems in academic communities often need help with issues such as manipulation, lack of adaptability to different scales of contributions, and the inability to account for the long-term impact of research. These systems also fail to incentivize a community-oriented approach where contributions are continuously and fairly rewarded, creating a competitive rather than collaborative environment.
Quantinar addresses the need for a robust reputation system in academic communities. The challenge is to develop a
system that fairly measures the relative value of contributions within an academic community, ensuring that these assessments are scalable, reflect the long-term value of contributions, and resist manipulation.
Method
Quantinar adopts CredRank, a variant of the PageRank algorithm, designed to map the complex network of contributions within a community. This system integrates temporal dynamics into the evaluation, allowing for the reputation score to adapt over time, reflecting the changing impact of contributions. CredRank provides a dynamic and community-driven approach to evaluating contributions, distributing “QNAR” tokens as a measure of reputation, which can then be used within the Quantinar ecosystem.
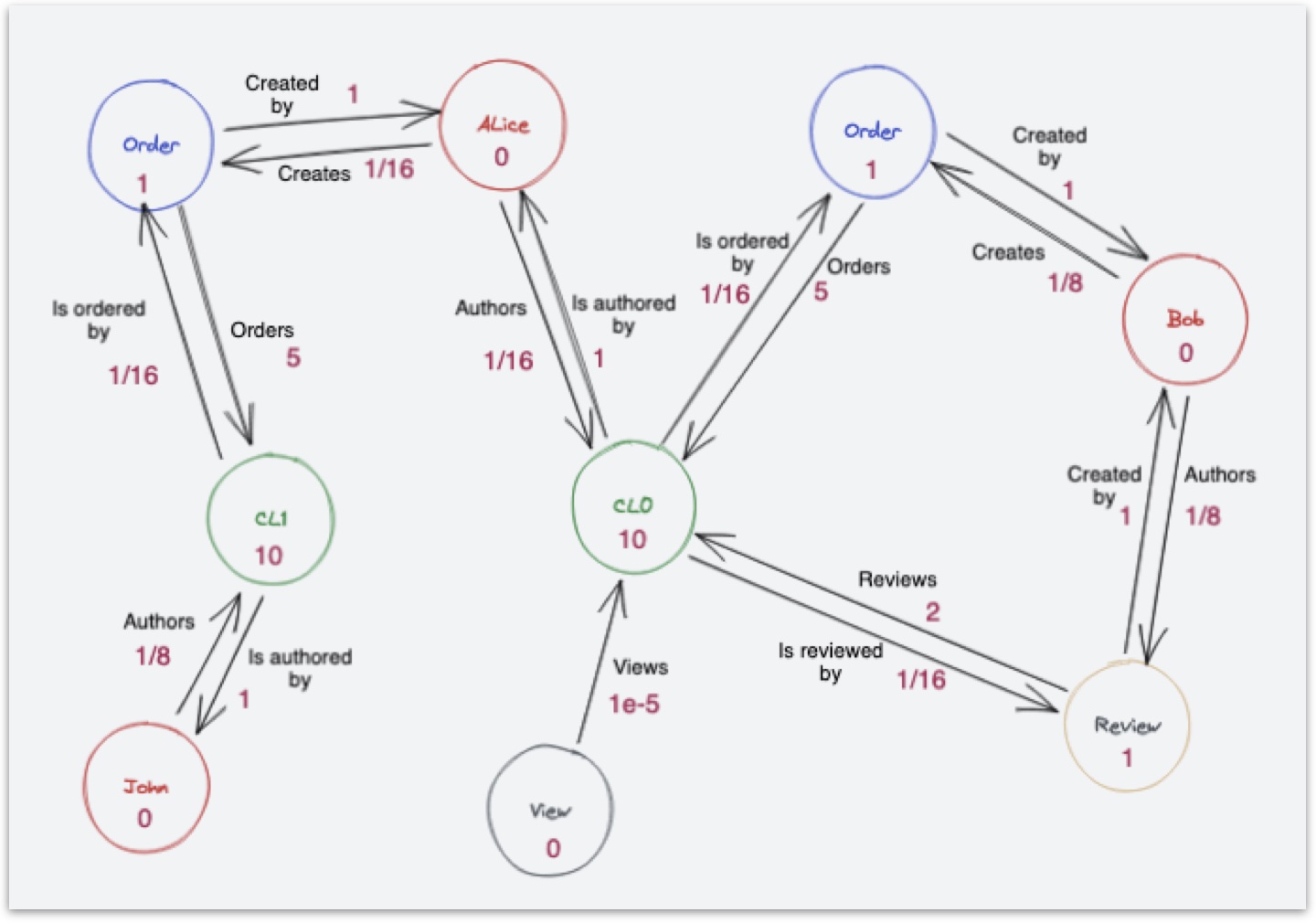
In detail, all contributions, and community members are mapped onto a directed graph \(G = ( \mathcal{V}, \mathcal{E}, \mathcal{W})\) where \(\mathcal{V} = \{s_0\} \cup \mathcal{A} \cup \mathcal{C} = \{v_i\}_ {1\leq i \leq n}\) is the set of \(n\) unique vertices mapping the seed node, contributions, and contributors which are connected with \(m\) directed edges, \(\mathcal{E} = \{e_{ij}\}_{(v_i,v_j) \in \mathcal{V}^2}\), where \(e_{ij}\) denotes the edge from parent vertex \(j\) to child vertex \(i\) and \(\mathcal{W}=(w_{ij})_{e_{ij}\in \mathcal{E}}\) with \(w_{ij} \geq 0\) is the set of \(m\) edges weights which are chosen by the community members in a heuristic manner. The weights have a strong influence on the PageRank computation and the final reward, thus they must ensure that contributions that require a lot of labor get rewarded more than simpler ones and when they are validated or reviewed by the community. Indeed, if a contribution \(j\) has multiple children, its score should be propagated forward to the most important child.
Contribution graph example
In a second step, each vertex \(i\) is indexed by a timestamp \(t\) corresponding to its appearance in Quantinar and denoted as \(v_{it}\). The history is then discretized in \(T\) fixed length periods (for example a week).
We define \(\mathcal{A}_k = \{v_{it},\ 1\leq i \leq n,\ 1\leq t \leq k,\ v_{it} \in \mathcal{A}\}\) as the set of vertices including all contributions until the date \(k\). We can easily retrieve the set of new contributions during the period \(k \geq 1\) with \(\mathcal{A}_k^{new} = \mathcal{A}_k \setminus \mathcal{A}_{k-1}\) and \(\mathcal{A}_0^{new} = \mathcal{A}_0\). At each period \(k\), we create the epoch contributor nodes that authored the new contributions in \(\mathcal{A}_k^{new}\), that is \(\mathcal{C}_k^{new} = \{v_{ik},\ 1\leq i \leq n\) if \(e_ {ij} \in \mathcal{E}, v_i \in \mathcal{C},\ v_j \in \mathcal{A}_k^{new}\}\). Thus the set of epoch contributor nodes until period \(k\) is defined as \(\mathcal{C}_k = \bigcup_{1\leq t \leq k} \mathcal{C}_k^{new}\). We add directed edges from the contributions in \(\mathcal{A}_k^{new}\) to their respective author(s) in \(\mathcal{C}_k^{new}\).
On top, webbing edges between previous and new epoch contributors are added with associated transition probability \(\gamma_f\) and \(\gamma_b\) connecting \(\forall v_i \in \mathcal{C}_{k-1}\), \(v_{ik-1}\) and \(v_{ik}\) frontward and backward, respectively. The webbing edges ensure that the reputation gained at previous epochs has inertia over time.
Finally, each epoch contributor node from \(\mathcal{C}_k\) is connected to its associated contributor node in \(\mathcal{C}\) with transition probability \(\beta\).
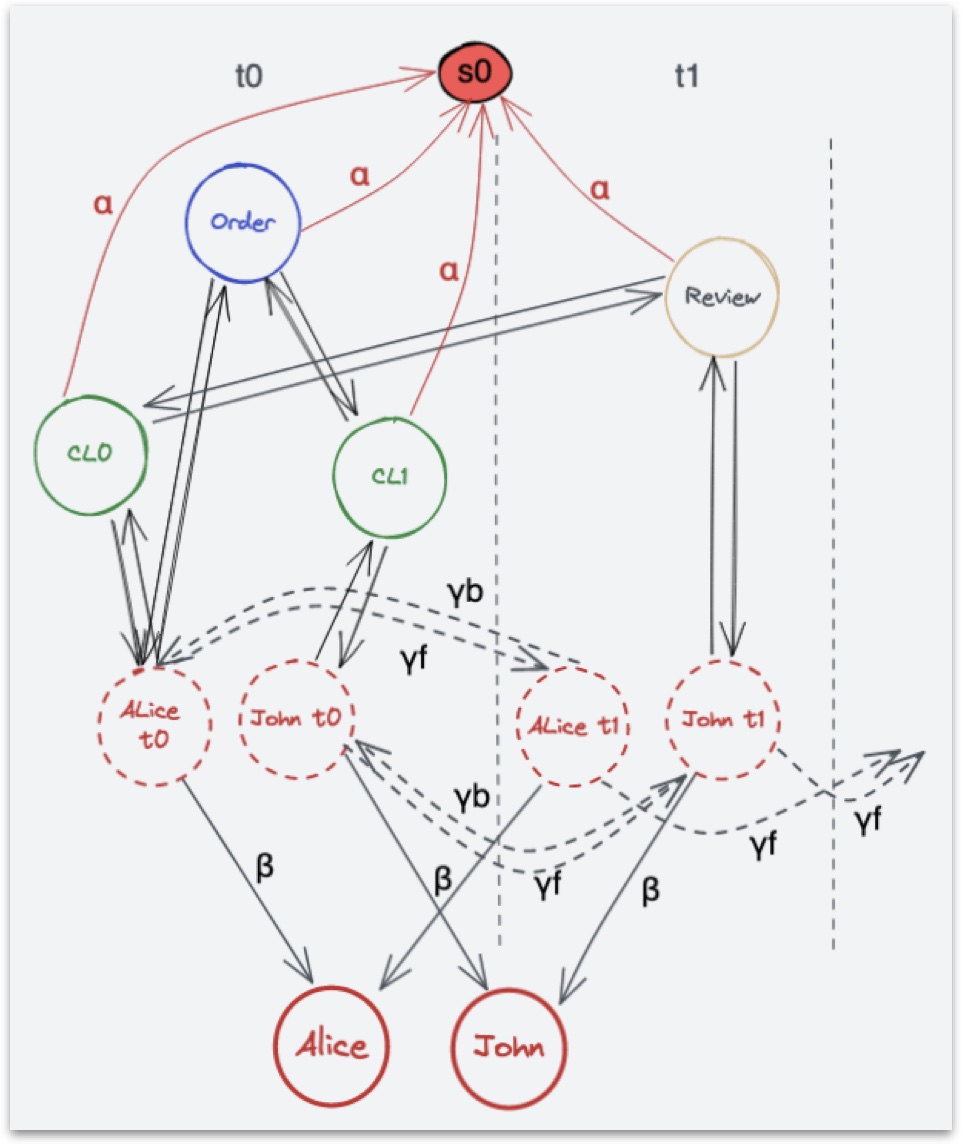Discretized Contribution graph example
Thanks to this graph, each contribution is connected to its associated contributor only through the epoch contributor node and not the global contributor node. That way, for any contributor \(i\) and period \(k \geq 1\), the PageRank score at a previous period \(k^{'} < k\) is easily accessible at the epoch contributor \(v_{ik}'\).
For any \(k,\ 1 \leq k \leq T\), we define the epoch contribution graph as \(G_k = (\mathcal{V}_k, \mathcal{E}_k, \mathcal{W}_k)\) where \(\mathcal{V}_k = \{s_0\} \cup \mathcal{A}_k \cup \mathcal{C}_k \cup \mathcal{C}\), \(\mathcal{E}_k = \{e_{ij}\}_{(v_i, v_j) \in \mathcal{V}_k^2}\) and \(\mathcal{W}_k=(w_{ij})_{e_{ij}\in \mathcal{E}_k}\).
The graph update is then given by:
We then solve the PageRank random surfer equations on \(G_k\) to obtain the node score at each period.
Results
The implementation of CredRank on Quantinar has shown that it effectively captures the dynamic nature of academic contributions. The system has demonstrated an ability to reward contributors not just for their immediate input but also for the ongoing relevance and utility of their work. This dynamic scoring system encourages contributors to focus on the quality and long-term impact of their research, fostering a more collaborative and supportive academic environment.
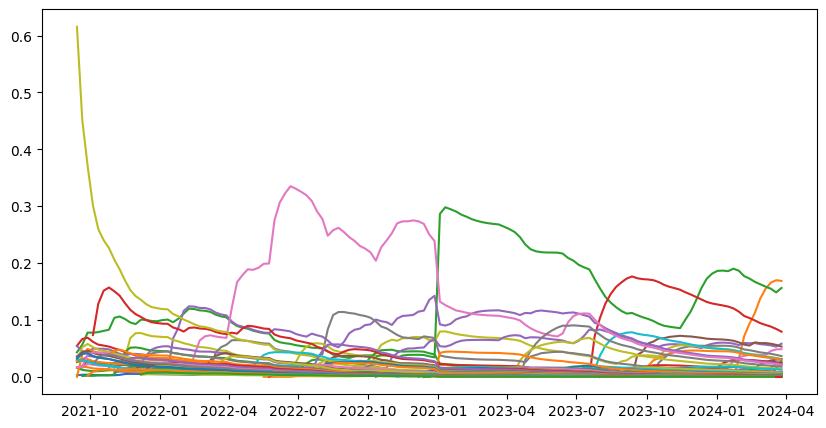QNAR score dynamics. Notes: The score has inertia over time which guarantees that the contributions from the previous period still have values today. Nevertheless, contributors need to consistently add contributions to keep up with new active contributors, which can be observed when comparing the olive and pink curves. Indeed, as the evaluation period is more recent, the score of the early contributor in Olive decreases at an inversely exponential rate from September 2021, as the user probably reduced its contribution to Quantinar. On the other hand, the user corresponding to the pink curve starts to be very active in March/April 2022 and his score increases drastically until he reaches the highest score in mid-July 2022.